一般に投資の世界ではリターンとリスクはトレードオフの関係にあり、より高いリターンを狙えばリスクが高くなり、より低いリターンに甘んじればリスクは低いものになるという。これは体感的にも、いろんな生活実感の中での例を挙げても説明出来る納得のいく話である。
リターンは誰にでも理解出来る。何%値上がりしたか、それを年率換算すると幾らになるかぐらいなので敢えて説明するまでもない。
問題はリスクの方。昔からリスクの説明については苦労した。何故なら、リスクという英語のイメージは「危険」であり、「リスクが高い」「ハイ・リターン」と言えば、危険がいっぱいという印象になってしまうからだ。
だが、投資の世界でいうリスクは、「危険」という語感のものとは少々異なり、「ブレ幅」のこと、すなわちリターンが上下にどの程度変動するかを示す指標として定義される。仮にリターン5%でリスクが5%ならば、そのリターンは0%から10%の間を変動する可能性があるという意味だと定義される。つまり危険ではなく、より儲かっても「リスク」ということだ。
ゴルフをされる方なら直ぐにイメージできると思われるが、第一打目では距離を求めるために、クラブはドライバーを振り回すことが多い。長い距離が狙える代わりに、右に左に大きくブレる可能性がある。それを嫌って、短めのアイアンを握れば、距離は控え目になるものの、その分、左右にブレる確率はグッと低くなる。正にこれがリターンとリスクの関係。
さて問題はここからである。リスクはどうやって、何を計算したものなのか、そこから何が分かるのか?ということである。
百聞は一見に如かず、実際に計算した例を下記の表で説明する。
まずある投資信託の過去6年間の利回りを調べたらa期の4%に始まり、f期の△4.5%まで様々な利回りがあったとしよう。8%儲かった時もあれば、△4.5%と凹んだ時もある。6年間を合計すると16.5%のリターンとなるが、平均値は2.75%である。つまり年平均のリターンは2.75%ということになる。
平均が2.75%の投資信託を買ったのに、ある時は8%も儲かり、翌年には△4.5%にも落ち込んだら驚くかもしれない。その為、予めリスクという形でそのブレ幅を計算し、平均値からどの程度乖離する場合があるかを示すのがリスク値の正体なのだが、実はこれは言い訳の材料として考え出されたと言っても過言ではない場合がある。下記の例は正にその好例となるが、それを知っておいて欲しいと思う。
<あるファンドの過去6年間の利回り推移>
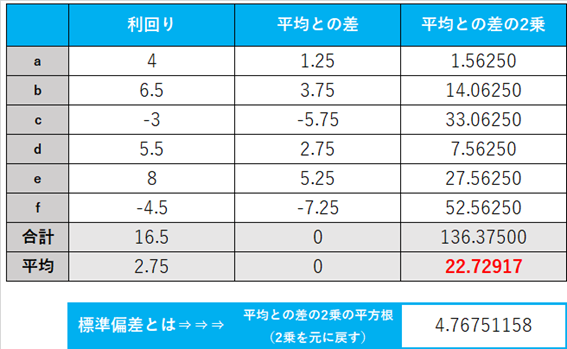
標準偏差を計算する方法は、①データの平均値と各データの差を計算することから始まる。表の真ん中の列である。当然合計しても、平均を計算してもゼロとなる。ただ問題はプラスの値もあれば、マイナスの値もあることである。②このプラスマイナスを無くして同じ土俵に載せるために、一旦2乗する。一番右側の列である。「マイナス×マイナス」はプラスになるからである。そして③その値の平均値を計算する。上の表では赤フォントで「22.72917」と表示されている数値である。
この値を数学では「分散」と呼ぶが、既にプラスマイナスを消すために一度2乗してあるので、④この平方根(√)を計算して元に戻した感じなのが標準偏差である。この場合、「4.76751158」というのが答えである。
この計算の基本的な意味は何かといえば、各データがどの程度平均値からバラついているかを理解しやすくするため、距離を測って数値化したのと同じ。だからマイナスの距離があっては困るので、一旦2乗して全てをプラスの値に変えて、そして平方根(√)を計算して元に戻してあるのである。標準偏差の計算方法は実は簡単である。
さて、このファンドのパフォーマンスをリターンとリスクという事だけで説明すると「過去6年間の平均リターンは2.75%で、リスク(時にボラティリティと呼ぶ)は約4.77%です。」と説明することが出来るのだが、皆さんそれで得心がいくだろうか?
リスクを標準偏差で表した場合、必ずその意味として付け加えられるセリフが「リスクとは、約2/3の確率で、その範囲内に収まるという意味です」という尤もらしい解説である。
しかし実際に今計算した例を見てみよう。
平均は2.75%で、リスクは4.77%とすると、△2.02%~7.52%の間に2/3の確率で収まっていないとならないが、6つのデータの内、実はaとbとdの3つしか収まっていない。つまり2/3ではなく、1/2しか無いのである。
行動経済学でいうところの儲かった場合と損した場合の人間の精神面に与えるインパクトは等金額ではないという理屈を持ち込めば、2/3の確率で、悪くても△2.02%に収まる筈がその2倍以上の△4.5%になった場合のそれは、同じく上限値の7.52%が8%になった場合と比べて遥かにダメージは大きいだろうと推察出来る。
なのにである、恐らくどこの金融機関に行って説明を聞いても、「リスクとは約2/3の確率でその範囲内に収まる振れ幅を示したものです」ということしか言われないであろう。実際、標準偏差の計算方法を知っているかさえも疑わしいケースが沢山あるのだから。
この問題の謎を解くカギは、マーコビッツという天才学者によって作られた「現代投資理論」と呼ばれる画期的な理論、リターンとリスクを定量化してポートフォリオ理論を展開したものに由来するのだが、実はそこには多くの仮定や前提がある。この標準偏差という考え方も正にその代表的なひとつである。
「正規分布」という言葉を聞かれたことがあるか、或いは記憶の片隅にある、という方は多いだろうと思う。昔は高校の数学Ⅱbで教えられていたので、文科系の人でも眠い目をこすりながら聞かれたかも知れない。正にこの「正規分布」という単語がカギである。
マーコビッツの「現代投資理論」の大前提には、全ての自然界の事象は正規分布に従うという前提がおかれているのである。正規分布とはどのような状態かを示したのが下の図である。
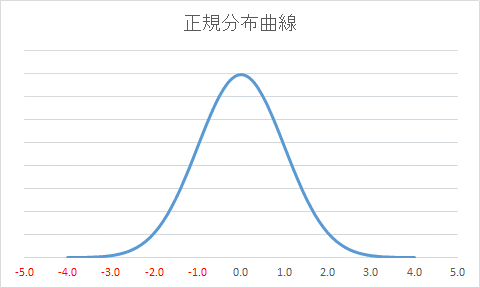
ご覧頂けるように、平均値を真ん中にして左右均等にスカートを広げたようにデータが散らばっている状態が正規分布であり、これはその外周を結んだ正規分布曲線を示している。
もうお気づきのように、世の中の事象はこのような「釣り鐘型の正規分布曲線」の中に納まるわけがない。学校で徒競走をさせても、算数のテストをしても、平均点は平均点でも、実際の生徒の成績のばらつきは平均値の周りに左右均等に集まりはしない。もしかすると平均値の辺りが一番少なくて、両サイドに二つのこぶのように山が出来ているかも知れない。
さて、結論をお伝えしよう。既にもう皆さんもお気づきの通り、標準偏差で計算したリスクという指標は、一見尤もらしくも思われるが、この程度の参考にしかならない数値だということである。だからリスクが高いとか、低いとか言っても、その数値自体にはこの程度の意味合いしかないものだと思って、この数値とはお付き合いされたら良いと思う。


